Index 인덱스
: 추가적인 쓰기 작업과 저장 공간을 활용해서 검색 속도를 향상시키기 위한 자료구조
Index 사용 동기
- 탐색을 위한 IO 연산 수 줄임
- insert 시, 다른 레코드를 뒤로 밀어야함. 최악의 경우 2*N/P만큼 IO 연산 필요
- 다중 속성 검색 시 데이터 공간 비효율적
=> index 가 필요!
NoSQL에서도 중요하다!
전통적인 데베와 달리 유저에게 많은 기능을 양보하였지만, 데이터의 검색 성능은 보장해주어야함.
B+Tree, Hash 등을 사용.
Indexs: High-level
인덱스는 특정 속성 값 또는 검색 Key를 통해 빠르게 찾음.
Primary key != search Key
(ex.Product(name, maker, price) 셋 모두가 검색 키 가능)
index: 검색 키와 데이터베이스 테이블의 행들을 매핑해주는 자료구조.
즉, 특정 키 값으로 관련 로그 빠르게 가져옴.
종류
1. primary index : 데이터 자체를 인덱스 안에 보유
2. secondary index : 해당 데이터가 저장된 위치를 가리키는 포인터만 저장
secondary index가 일반적으로 많이 활용됨.
대부분 실제 쿼리는 하나의 데이터에 대해 여러 인덱스 사용하기 때문.
index에서의 연산
- 검색 : 검색 키 속성에서 요구조건에 맞는 레코드를 빠르게 찾는 것.
- 삽입/제거 : 빠르게 이루어져야함. Bulk load /delete 와 같은 일괄 로드, 삭제 필요
index가 없는 상황에서 데이터 검색이 얼마나 비효율적일까?
SELECT *
FROM Russian_Novels
WHERE Published > 1867
데이터를 처음부터 끝까지 탐색해야해 => 비효율적!

출판 연도 뿐만 아니라 여러 개의 인덱스를 각각의 속성을 기준으로 가지면,
여러 속성에 대한 빠른 검색 가능
=> 쿼리 최적화.
실제로는 인덱스가 table이 아닌 B+tree로 구성되어 있음.
Composite Keys(복합키)
: 하나의 인덱스에 여러 속성을 넣어 사용하는 것.

<Age, Sal> : Age 먼저 정렬 후, Age에 따른 Salary 값 인덱스
이 인덱스를 선택할 경우,
- 값이 일치하는 질의 (Age=12 and Sal=90?),
- 조건부 범위 질의 (Age = 5 and Sal>5?)
에 대해서 처리 가능
<Sal, Age> : Salary 먼저 정렬 후, Salary 값에 따른 Age 값 인덱스
현재의 조건부 범위 질의 검색이 잘 작동되지 않을 수 있음.
=> 단순히 속성을 '결합'하는 것이 아닌, 질의의 패턴을 예측하고 그에 맞는 정렬 순서를 선택하자.
복합키 장단점
장점:
- 잘 설계되면, 단일 인덱스만으로도 여러 조건을 만족하는 검사 가능
- 특정 질의 자주 발생 시, 그 질의에 맞는 인덱스 제작 시 쿼리 효율성 상승
단점:
- 복합키의 순서가 질의와 잘 맞지 않으면 제대로 사용할 수 없음.
- 여러 속성 모두 대비하기 위해서는 인덱스를 너무 많이 만들어서 저장 공간과 유지 비용 증가.
=> 내가 주로 수행할 질의는 어떠한 속성을 주로 사용? 하는지 생각하면서 설계
즉, 데이터와 질의 패턴에 따라 인덱스 다르게 설계됨.
Covering indexes
: 특정 질의에서 필요한 모든 속성 이미 인덱스가 가짐.
테이블에 접근할 필요없이 인덱스 내에서 검색 가능.

SELECT Published, BID
FROM Russian_Novels
WHERE Published > 1867
필요한 속성 Published와 BID 모두를 인덱스에서 가지고 있음.
여기서 필요한 속성은?
SELECT절과 WHERE절에 언급된 속성들을 합친 것!
장점
- Disk IO 크게 감소
- 응답 속도 매우 빨라짐.
=> DBMS가 쿼리 최적화 시 적극 사용!
Index 구조
1. B-Trees
범위/정렬 질의에 유용.
일부 오래된 데베는 B-Tree만 지원하기도 했음.
우리는 이 트리의 변형구조 B+Trees에 대해 알아볼것임.
2. Hash Table
정확한 일치 질의에 유용. 범위 질의에는 부적합.
linear hasing, extendible hashing
모두 디스크 IO를 고려한 설계임! (IO aware)
B+Tree에서 어떻게 삽입/삭제하는지, 그때의 밸랜스는 어떻게 되는지를 중점으로 보자!
B+ Tree

- 한 노드가 여러 개의 자식을 가질 수 있는 다진 트리임.
- 하나의 노드가 하나의 디스크 페이지와 1대1 대응 -IO aware
- 항상 밸런스 유지. 모든 leaf 노드가 같은 깊이(층)에 존재.
- leaf 노드는 모두 linked list로 연결되어 있음. => 범위 검색에서 강력한 성능 발휘!!
- 정렬뿐만 아닌, 삽입/삭제 문제를 디스크 구조를 고려하여 효율적으로 처리하여 실용적.
기본 내부 구조
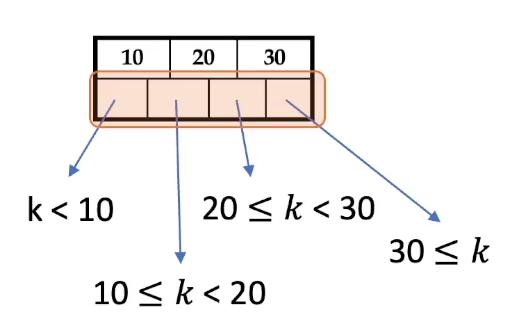
- degree : 한 노드가 가질 수 있는 최소, 최대 키 수를 결정하는 기준
degree = 포인터의 개수.
- 루트 노드 (root node)
제일 위의 노드. Key 최소 1개 ~ 최대 2개의 key 가질 수 있음.
key 개수 : 1 ~ 2d
- 내부 노드 (non-leaf node) :
키 값 저장.
n개의 key가 있다면 (n+1)개의 노드를 가질 수 있음.
key 개수 : 최소 d개 ~ 최대 2d개

- 리프 노드 (leaf node)
데이터 저장.
특정 key 값과 함께 그 키에 해당하는 실제 데이터의 위치 데이터 함께 저장.
데이터베이스의 특정 행 가리키는 포인터 역할
데이터 검색의 최종 단계
linked list 구조. 다음 리프 노드를 가리키는 포인터 추가로 가짐. => 이를 통해 순차적 검색 가능.(범위 질의)
다시 루트노드로 돌아갈 필요없이, 한 번 도달한 리프 노드만으로도 탐색 가능.
key 개수 : d~2d 개의 key
=> 단순히 key를 정하는 것 아닌, 우리가 원하는 실제 데이터를 찾아가게 하는 포인터를 저장하고 있음.
리프 노드는 구간 정보 담김.
각 구간에 포함된 자식노드로 포인터가 존재.
B+ Trees에서의 Key 값 검색
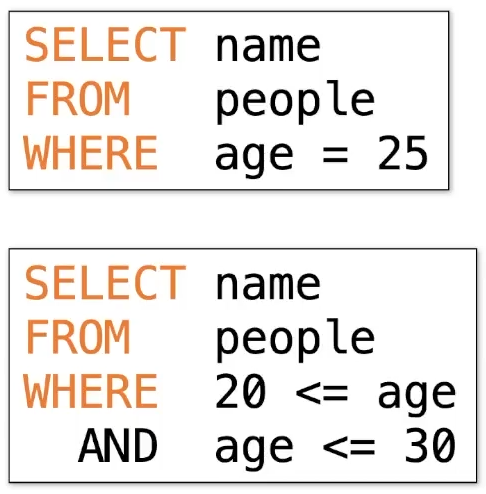
"age를 기준으로 인덱스를 설계해야겠네"
- 첫번째 쿼리
: age 값이 25인 노드 찾을 때까지 루트 노드에서부터 내려감.
- 두번째 쿼리
: age 20 찾기. 이후 linked list로 순차적 30 아래 age 까지 찾기.
Q. range query, [30, 85] 범위의 key들을 검색해보자.

- 30 < 80 -> [20, 60] -> [30, 40] -> 30 찾기 성공 -> 디스크로 내려보냄.
- 30부터 linked list로 84까지 순차적 탐색 및 디스크로 내려보냄.
B+Tree의 설계
"d의 크기를 얼마로 하면 좋을까?"
하나의 블럭/페이지 용량에 맞는 노드 필요.
전체 key 크기 + 전체 pointer 크기 = (d-1)*key 크기 + d*pointer 크기 <= block 크기
노드 안의 key, pointer 들의 크기를 더하여 블럭과 비교해봄으로써,
블럭 안의 degree 크기 범위를 유추할 수 있다!
**기억해야하는 점
key 크기 = pointer 크기 = (d-1)
예시:
key 크기 = 4bytes
pointer 크기 = 8bytes
block 크기 = 4096 bytes
- (d-1)*4 + d*8 <= 4096 => d <= 341
최대 341개의 자식을 가질 수 있다!
Oracle의 경우 블럭의 크기를 64KB까지 허용.
64KB = 2^16byte
- (d-1)*4 + d*8 <= 2^16 => d <= 2730
fanout(자식 갯수)이 높아질수록, tree의 깊이는 낮아짐 => IO 횟수 줄어듬
결론, degree를 최대 크기로 정할수록 최적화
B+Tree 다른 트리보다 훨씬 높은 fanout을 가짐.
| 잠시만! B <-> byte 변환 방법 단위가 byte, K, MB, GB로 점점 커질수록 1024배가 된다. 1KB = 1024byte 64KB = 64 * 1024 = 2^16 byte 1MB = 1024^2byte = 2^20 byte 1TB = 1024^4byte = 2^40 byte |
높은 fanout을 가짐으로써 얻는 이점
- fanout : 한 노드가 가리킬 수 있는 자식의 노드의 수.
- B+ Tree의 fanout 범위 : (d+1)~(2d+1) => 한 노드가 훨씬 더 많은 자식 노드 가리킬 수 있음.
- 결과적으로, tree의 전체 높이가 낮아지면서, 특정 데이터를 찾기 위해 디스크가 읽어야하는 페이지 수가 줄어듬!
=> 페이지 IO 연산 수 극소!!!
예시. 아래와 같은 상황일 때 B+Tree의 높이는 얼마일까? (file-factor = 1 포함)
데이터 크기 : 1TB = 2^40 byte
한 블럭 크기 : 64KB 페이지 = 2^16 byte
- 총 페이지 개수 = 2^40 / 2^16 = 2^24 = 16백만 개
- oracle에서 64KB의 d : 2730
- 그에 따른 fanout, 자식의 수 : (2d + 1) = 5461
- Level 1 = 5461
- Level 2 = 5461 ^2 ~= 30백만 개
- 최대 3번의 IO 연산 필요!
B+Tree 예시
노드 꽉 찼을 때의 시나리오
새로운 데이터가 삽입되려면 노드가 분리되어야 함.
-> copy 발생 -> 성능 저하
fill-factor
: 새로운 데이터를 삽입할 때 여유롭게 하기 위해 일부만 채워넣는 것.
일반적으로 2/3 정도 채워넣음.
=> 빈번하게 삽입이 되더라도 새로운 노드를 너무 자주 만들지 않도록.
- d=100. fill-factor: 67%
- anout = 2d+1 = 201가 아닌 133이 됨.
- fanout 값이 넘으면 분리가 됨.
- 성능
- 높이 4 저장 가능한 레코드 개수: 133^4
- 높이 3 저장 가능한 레코드 개수: 133^3
- 버퍼 양에 대한 트리 레벨
- level 1 = 1page = 8KB
- level 2 = 133page = 133*8 = 1Mb
- level 3 = 17689page = 133Mb
=> 메모리 최대한 활용하면서 IO 줄임.
IO 비용 추정하는 수학적 모델
- f: fanout
- N: 인덱스해야할 페이지 총 갯수
- F: file-factor

=> fanout 크고, fill-facotr 높을수록 tree 높이 낮아짐.
메모리 고려한 검색 비용 추정
한 번만 search하는 경우(exact query),
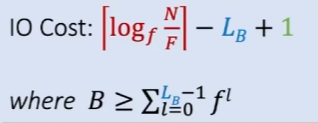
버퍼의 크기 고려!
B+Tree의 정확한 key 값을 검색할 때 발생하는 IO 비용을 정량적으로 계산
- B : 시스템에 주어진 버퍼 페이지 개수
- L_B : 메모리에 이미 들어와있는 level 갯
- f^l : 각 레벨에 필요한 노드의 수
우리는 사용 레벨 일부를 버퍼에 저장할 수 있을 것이다.
우리가 어떤 레벨까지 저장해야하는데, 거기에 필요로하는 버퍼 크기 이하로 저장할 수 있다.
요약해서,
- 우리는 레벨당 하나의 페이지를 읽는다.
- 하지만, 우리가 버퍼에 넣을 수 있는 레벨은 free이다.
- 마침내 우리는 실제 레코드를 읽는다!
범위 search하는 경우 (range query),
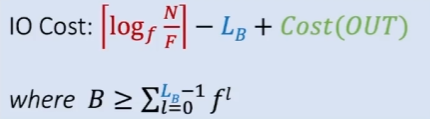
처음 위치까지는 동일.
범위의 마지막 위치까지 쫓아가는 것은 Cost(OUT) 으로 표현.
레벨의 높이에서 필요로 하는 IO 수.
메모리에 이미 들어와있는 level 갯수.
실제 데이터가 순차적으로 저장이 되어 있지 않다면 어떻게 동작할까?
Clustered Indexes
: 인덱스와 실제 데이터가 동일한 정렬 순서를 가질 경우를 말함.
Unclustered Indexes
: 인덱스와 실제 데이터가 다른 정렬 순서를 가지는 경우
Clustered는 순차적 읽기가 가능하지만,
Unclustered는 매번 처음부터 다시 읽어야함. 왔다갔다.
=> 비용 굉장히 커짐!
=> exact search 에서는 변화 없지만, range search에서는 어마어마한 차이 발생!
B+Tree 속도와 구조 유지 요약
- 정확한 검색과 거의 동일한 비용으로 수행.
- tree 높이에 비례하는 경로 탐색만 거치면 삽입 가능.
- 삽입 과정 중 트리의 균형 자동으로 유지 (ex. 삽입으로 인해 노드가 가득차면 분리가 되고, 이 상위 노드가 분할키로 전파가 되어서 트리 전체가 항상 균형 유지하도록 만듬)
- 단일 삽입에도 빠르지만, 여러개의 연속 삽입, 대량의 레코드 삽입에 분리(split) 많이 발생 -> 병목 발생 가능 => 대규모 삽입에는 전용 전략(fill-factor)이 필요하다!
균형 유지와 검색 성능을 동시에 유지하는 것.
Bulk Loading
: 정렬된 데이터를 바탕으로 한 번에 여러 키 삽입하는 방식
일반적인 삽입 방식처럼 하나씩 삽입 후 split은 비효율적
=> 트리를 한 번에 구성하자!

1. 정렬된 키값 데이터를 가지고 leaf 노드를 왼쪽부터 차례로 채움.
2. 한 leaf 노드에 들어갈 수 있는 key 수(L)를 기준으로 잘라서 노드를 생성.
3. leaf 노드끼리는 오른쪽 포인터로 연결.
4. 각 leaf 노드에서 첫번째 키를 부모 내부 노드에 key로 올림.
해당 key는 오른쪽 자식이 시작하는 키
ex. 각 내부노드가 가질 수 있는 자식 수 3일때,
leaf1의 첫 키 2, leaf2의 첫 키 12 -> 내부 노드: [12], 자식 노드 : [leaf1, leaf2]
내부 노드에 자식 많아지면 다시 상위 내부노드 생성
5. 내부 노드를 위로 올리는 작업 반복해서 루트 노드까지 생성
삽입 시 발생할 수 있는 Merge, Split에 대한 연산 부가 없이도 쉽게 가능.
'학교 공부' 카테고리의 다른 글
| [데이터베이스] 트랜잭션 (0) | 2025.06.12 |
|---|---|
| [운영체제] 파일 시스템 (1) (3) | 2025.06.08 |
| 36장~37장 I/O Devices와 Hard_Disk_Drives (0) | 2025.05.13 |